10.28. Numerical Input Problem¶
Note
EdX offers full support for this problem type.
The numerical input problem type is a core problem type that can be added to any course. At a minimum, numerical input problems include a question or prompt and a response field for a numeric answer. By adding hints, feedback, or both, you can give learners guidance and help when they work on a problem.
- Overview
- Adding a Numerical Input Problem
- Adding a Tolerance, Multiple Correct Responses, or a Range
- Adding Feedback to a Numerical Input Problem
- Adding Hints to a Numerical Input Problem
- Awarding Partial Credit in a Numerical Input Problem
- Add Text after the Numeric Response Field
- Numerical Input Problem OLX Reference
For more information about the core problem types, see Working with Problem Components.
10.28.1. Overview¶
In numerical input problems, learners enter numbers or specific and relatively simple mathematical expressions to answer a question. The LMS automatically converts the answer that learners enter into a symbolic expression that appears below the response field.
Responses for numerical input problems can include integers, fractions, and constants such as pi and g. Responses can also include text representing common functions, such as square root (sqrt) and log base 2 (log2), as well as trigonometric functions and their inverses, such as sine (sin) and arcsine (arcsin). For these functions, learners enter text that is converted into mathematical symbols. The following example shows a response entered by a learner and the numerical expression that results.
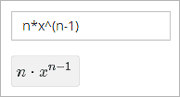
For more information about how learners enter expressions, see math formatting in the EdX Learner’s Guide or Completing Mathematical and Scientific Assignments in the Open edX Learner’s Guide.
Some of the options for numerical input problems include the following.
- You can specify a correct answer explicitly or use a Python script.
- You can specify a margin of error, or tolerance, for the answers to numerical input problems so that learners’ responses do not have to be exact.
Note
You can make a calculator tool available to your learners on every unit page. For more information, see Calculator Tool.
10.28.1.1. Example Numerical Input Problem¶
In the LMS, learners enter a value into a response field to complete a numerical input problem. An example of a completed numerical input problem follows.
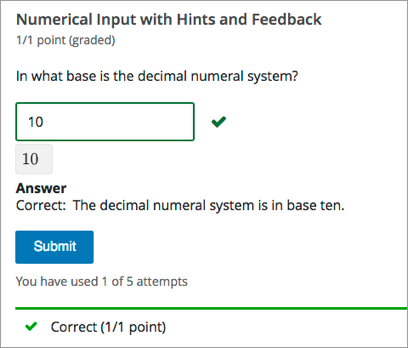
To add the example problem illustrated above, in Studio you use the simple editor to enter the following text and Markdown formatting.
>>In what base is the decimal numeral system?<<
=10 {{The decimal numeral system is in base ten.}}
The open learning XML (OLX) markup for this example numerical input problem follows.
<problem>
<numericalresponse answer="10">
<label>In what base is the decimal numeral system?</label>
<formulaequationinput/>
<solution>
<div class="detailed-solution">
<p>Explanation</p>
<p>The decimal numeral system is base ten.</p>
</div>
</solution>
</numericalresponse>
</problem>
10.28.1.2. Analyzing Performance on Numerical Input Problems¶
For the numerical input problems in your course, you can use edX Insights to review aggregated learner performance data and examine submitted answers. For more information, see Using edX Insights.
10.28.2. Adding a Numerical Input Problem¶
You add numerical input problems in Studio by selecting the Problem component type and then using either the simple editor or the advanced editor to specify the prompt and the acceptable answer or answers.
Note
You can begin work on the problem in the simple editor, and then switch to the advanced editor. However, after you save any changes you make in the advanced editor, you cannot switch back to the simple editor.
Before you add a numerical input problem, consider the following features and limitations of the simple and advanced editors.
- If your problem text contains italics, bold, or special characters, the
simple editor does not support these values. Use the advanced editor to add
an HTML paragraph (
<p>) element and HTML formatting tags as needed. - If your problem contains a Python script, use the advanced editor.
For example, you must use the advanced editor to define the following numerical input problem. It contains two questions, one of which relies on character formatting, and the other that uses a Python script.

The OLX for this example follows.
Note
The second question in the following example includes a Python
script. When you add a script to a problem component, do not add to or change
its internal indentation. A “jailed code” error message appears when you save
the problem in Studio if the <script> element is indented.
<problem>
<numericalresponse answer="9.80665">
<p>Enter the value of the standard gravity constant <i>g</i>,
measured in m/s<sup>2</sup>.</p>
<label>What is the answer to the question above?</label>
<description>Give your answer to at least two decimal places.</description>
<responseparam type="tolerance" default="0.01" />
<formulaequationinput />
<script type="loncapa/python">
computed_response = math.sqrt(math.fsum([math.pow(math.pi,2), math.pow(math.e,2)]))
</script>
<solution>
<div class="detailed-solution">
<p>Explanation</p>
<p>The standard gravity constant is defined to be precisely
9.80665 m/s<sup>2</sup>. This is 9.80 to two decimal places.
Entering 9.8 also works.</p>
</div>
</solution>
</numericalresponse>
<numericalresponse answer="$computed_response">
<label>What is the distance in the plane between the points (pi, 0)
and (0, e)?</label>
<description>You can type math.</description>
<responseparam type="tolerance" default="0.0001" />
<formulaequationinput />
<solution>
<div class="detailed-solution">
<p>Explanation</p>
<p>By the distance formula, the distance between two points in
the plane is the square root of the sum of the squares of the
differences of each coordinate. Even though an exact numerical
value is checked in this case, the easiest way to enter this
answer is to type <code>sqrt(pi^2+e^2)</code> into the editor.
Other answers like <code>sqrt((pi-0)^2+(0-e)^2)</code> also
work.</p>
</div>
</solution>
</numericalresponse>
</problem>
For more information about including a Python script in a problem, see Write-Your-Own-Grader Problem.
10.28.2.1. Use the Simple Editor to Add a Numerical Input Problem¶
When you add a numerical input problem, you can choose one of these templates.
- Numerical Input
- Numerical Input with Hints and Feedback
These templates include the Markdown formatting that you use in the simple editor to add a problem without, or with, hints and feedback.
To use the simple editor to add a problem, follow these steps.
In the unit where you want to create the problem, under Add New Component select Problem.
From the list of Common Problem Types, select the type of problem you want to add. Studio adds a template for the problem to the unit.
Select Edit. The simple editor opens to a template that shows the Markdown formatting that you use for this problem type.
Replace the guidance provided by the template to add your own text for the question or prompt, answer options, explanation, and so on.
To format equations, you can use MathJax. For more information, see Using MathJax for Mathematics.
Select Settings to provide an identifying Display Name and define settings for the problem. For more information, see Defining Settings for Problem Components.
Select Save.
10.28.2.2. Use the Advanced Editor to Add a Numerical Input Problem¶
You can use the advanced editor to identify the elements of a numerical input problem with OLX. For more information, see Numerical Input Problem OLX Reference.
To use the advanced editor to add a problem, follow these steps.
Follow steps 1-3 for creating the problem in the simple editor.
Select Advanced Editor. The advanced editor opens the template and shows the OLX markup that you can use for this problem type.
Replace the guidance provided by the template to add your own text. For example, replace the question or prompt, answer options, and explanation.
To format equations, you can use MathJax. For more information, see Using MathJax for Mathematics.
Update the OLX to add optional elements and attributes required for your problem.
Select Settings to provide an identifying Display Name and define settings for the problem. For more information, see Defining Settings for Problem Components.
Select Save.
10.28.3. Adding a Tolerance, Multiple Correct Responses, or a Range¶
To give learners the option to receive full credit for a close approximation of the correct answer, and to support a wide range of possible correct numerical answers, you can specify a tolerance for the correct answer, multiple individual correct answers, or a range of values to mark as correct for the numerical input problem type.
10.28.3.1. Adding a Tolerance¶
You can specify a margin of error or tolerance for learner responses. You can specify a percentage, number, or range.
10.28.3.1.1. Add a Tolerance in the Simple Editor¶
To add a tolerance in the simple editor you use the following Markdown formatting.
- To specify a number on either side of the correct answer, after the answer
value add
+-{number}. For example, to include a tolerance of 5, add+-5. - To specify a percentage on either side of the correct answer, after the
answer value add
+-{number}%. For example, to include a 2% tolerance, add+-2%.
10.28.3.1.2. Add a Tolerance in the Advanced Editor¶
To add a tolerance in the advanced editor you include a <responseparam>
element with a type="tolerance" attribute and a default attribute set
to either a number or a percentage value.
The following example shows a problem with a decimal tolerance.
<problem>
<numericalresponse answer="ANSWER (NUMBER)">
<label>Question text</label>
<responseparam type="tolerance" default=".02" />
<formulaequationinput />
</numericalresponse>
</problem>
The following example shows a problem with a percentage tolerance.
<problem>
<numericalresponse answer="ANSWER (NUMBER)">
<label>Question text</label>
<responseparam type="tolerance" default="3%" />
<formulaequationinput />
</numericalresponse>
</problem>
10.28.3.2. Adding Multiple Correct Responses¶
You can specify more than one specific, correct response for numerical input problems. To do this, you can use the simple editor or the advanced editor.
If you specify multiple correct responses, you cannot also specify a tolerance, a range, or a text string as correct answers. For example, when you define multiple correct responses, you can specify a numeric value for each correct answer but not a tolerance, range, or text string.
10.28.3.2.1. Add Multiple Correct Responses in the Simple Editor¶
To specify additional correct responses in the simple editor, include
or= before each additional correct response.
>>How many miles away from Earth is the sun?||Use scientific notation to answer.<<
= 9.3*10^7
or= 9.296*10^7
10.28.3.2.2. Add Multiple Correct Responses in the Advanced Editor¶
To specify an additional correct response in the advanced editor, within the
<numericalresponse> element add the <additional_answer /> element with
an answer="" attribute value.
<problem>
<numericalresponse answer="9.3*10^7">
<label>How many miles away from Earth is the sun?</label>
<description>Use scientific notation to answer.</description>
<additional_answer answer="9.296*10^7"/>
<formulaequationinput/>
</numericalresponse>
</problem>
10.28.3.3. Specifying an Answer Range¶
You can specify an answer range so that any learner response within that range
is marked correct. To format an answer range, you provide the starting and
ending values and then separate them with a comma character (,). You then
surround the range with bracket ([ ]) or parentheses characters (( )),
or a combination of one bracket and one parenthesis.
- Use a bracket to include the number next to it in the range, as in a less than or equal to, or greater than or equal to, inequality.
- Use a parenthesis to exclude the number from the range, as in a less than or greater than inequality.
For example, to identify the correct answers as 5, 6, or 7, but not 8, specify
[5,8). To identify the correct answers as 6, 7, and 8, but not 5, specify
(5,8].
To specify a range in the simple editor, you enter the complete, formatted
range after the equals sign: =[5,8) or =(5,8].
To specify a range in the advanced editor, you enter the complete, formatted
range in the <numericalresponse> element as the value for the answer
attribute: <numericalresponse answer="[5,8)"> or <numericalresponse
answer="(5,8]">
10.28.4. Adding Feedback to a Numerical Input Problem¶
For an overview of feedback in problems, see Adding Feedback and Hints to a Problem. In numerical input problems, you can provide feedback for correct responses. If you define multiple correct responses, you can define feedback for each response.
Note
You cannot provide feedback for incorrect answers in numerical input problems.
In numerical input problems, use feedback to reinforce the process used to arrive at the correct answer.
10.28.4.1. Configure Feedback in the Simple Editor¶
You can configure feedback in the simple editor. When you add a numerical input problem, select the template Numerical Input with Hints and Feedback. This template has example formatted feedback that you can replace with your own text.
In the simple editor, you configure feedback for a numerical input problem with the following Markdown formatting.
=Correct Answer {{Feedback for the correct answer.}}
For example, the following problem has feedback for the correct answer.
>>What is the arithmetic mean for the following set of numbers? (1, 5, 6, 3, 5)<<
=4 {{The mean for this set of numbers is 20 / 5 which equals 4.}}
If you define multiple correct responses, you can define feedback for each response.
10.28.4.2. Configure Feedback in the Advanced Editor¶
In the advanced editor, you configure answer feedback with the following syntax.
<problem>
<numericalresponse answer="Correct Answer">
<label>Question text</label>
<formulaequationinput />
<correcthint>Feedback for the correct answer</correcthint>
</numericalresponse>
</problem>
For example, the following problem has feedback for the correct answer.
<problem>
<numericalresponse answer="4">
<label>What is the arithmetic mean for the following set of numbers?
(1, 5, 6, 3, 5)</label>
<formulaequationinput />
<correcthint>The mean for this set of numbers is 20 / 5 which equals 4.</correcthint>
</numericalresponse>
</problem>
If you define multiple correct responses, you can define feedback for each response.
10.28.4.3. Customizing Feedback Labels¶
By default, the feedback label shown to learners is Correct . If you do not define a feedback label, learners see this term when they submit a correct answer, as in the following example.
Correct: The mean for this set of numbers is 20 / 5 which equals 4.
You can configure the problem to override the default label. For example, you can configure a custom label for the answer.
Good job: The mean for this set of numbers is 20 / 5 which equals 4.
Note
The default label, Correct, displays in the learner’s requested language. If you provide a custom label, it displays as you define it to all learners. It is not translated into different languages.
10.28.4.3.1. Customize a Feedback Label in the Simple Editor¶
In the simple editor, you configure a custom feedback label with the following syntax.
=4 {{Label:: Feedback}}
That is, you provide the label text, followed by two colon (:) characters, before the feedback text.
For example, the following feedback is configured to use a custom label.
=4 {{Good Job:: The mean for this set of numbers is 20 / 5 which equals 4.}}
10.28.4.3.2. Customize a Feedback Label in the Advanced Editor¶
In the advanced editor, you configure custom feedback labels with the following syntax.
<correcthint label="Custom Label">Feedback</correcthint>
For example, the following feedback is configured to use a custom label.
<correcthint label="Good Job">The mean for this set of numbers is 20 / 5 which equals 4.</correcthint>
10.28.5. Adding Hints to a Numerical Input Problem¶
You can add hints to a numerical input problem using the simple editor or the advanced editor. For an overview of hints in problems, see Adding Feedback and Hints to a Problem.
10.28.5.1. Configure Hints in the Simple Editor¶
In the simple editor, you configure hints with the following syntax.
||Hint 1||
||Hint 2||
||Hint n||
Note
You can configure any number of hints. The learner views one hint at a time and views the next one by selecting Hint again.
For example, the following problem has two hints.
||A fruit is the fertilized ovary from a flower.||
||A fruit contains seeds of the plant.||
10.28.5.2. Configure Hints in the Advanced Editor¶
In the advanced editor, you add the <demandhint> element immediately before
the closing </problem> tag, and then configure each hint using the
<hint> element.
.
.
.
<demandhint>
<hint>Hint 1</hint>
<hint>Hint 2</hint>
<hint>Hint 3</hint>
</demandhint>
</problem>
For example, the following OLX for a multiple choice problem shows two hints.
.
.
.
</multiplechoiceresponse>
<demandhint>
<hint>A fruit is the fertilized ovary from a flower.</hint>
<hint>A fruit contains seeds of the plant.</hint>
</demandhint>
</problem>
10.28.6. Awarding Partial Credit in a Numerical Input Problem¶
You can configure a numerical input problem to award partial credit to learners who submit an answer that is close or related to the correct answer. You must use the advanced editor to configure partial credit.
In the following example, the learner entered an answer that was close to the correct answer and received partial credit.
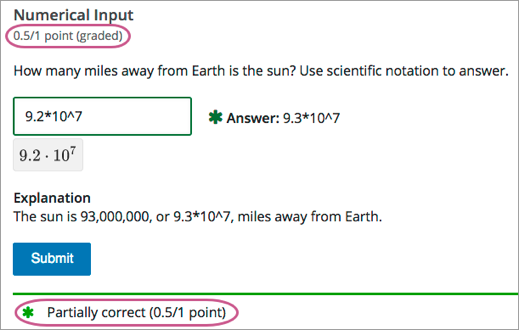
For an overview of partial credit in problems, see Awarding Partial Credit for a Problem.
You can use the following methods to award partial credit in a numerical input problem.
Note
You can use these methods of awarding partial credit individually or in combination.
10.28.6.1. Identifying Close Answers¶
You can configure a numerical input problem so that answers that are close to the correct answer receive partial credit.
To do so, you configure the tolerance for incorrect answers. Learners receive partial credit for close answers based on the tolerance. By default, the tolerance is multiplied by 2 and the following rules are applied.
- An answer within the tolerance receives 100% of the points for the problem.
- An answer within or equal to 2x of the tolerance receives 50%.
- An answer more than 2x the outside of the tolerance receives 0%.
You can optionally specify a different multiplier for the tolerance. For example, you could set the multiplier to 3. In this case, the following rules apply.
- An answer within the tolerance receives 100% of the points for the problem.
- An answer within or equal to 3x of the tolerance receives 50%.
- An answer more than 3x outside of the tolerance receives 0%.
10.28.6.1.1. Configure Close Answers for a Numerical Input Problem¶
To configure a numerical input problem to award partial credit for close answers, you add the following attributes to the problem XML.
Add the
partial_credit="close"attribute to the<numericalresponse>element.You can use close answers in combination with a list. Set the attribute to
partial_credit="close,list".Optionally, add the
partial_rangeattribute to the<responseparam>element and set its value to the tolerance multiplier. If you do not set thepartial_rangeattribute, 2 is used as the tolerance multiplier.
For example, the following OLX shows a numerical problem that provides partial credit for close answers.
<problem>
<numericalresponse answer="9.3*10^7" partial_credit="close">
<label>How many miles away from Earth is the sun?</label>
<description>Use scientific notation to answer.</description>
<formulaequationinput/>
<responseparam type="tolerance" default="1%" partial_range="3"/>
</numericalresponse>
</problem>
10.28.6.2. Awarding Partial Credit for Answers in a List¶
For some numerical input problems, mistakes do not help a learner arrive at the correct answer. For example, a small mistake can lead to negative instead of positive results, or to an answer that is off by a square root or numerical factor.
For these types of problems, you can configure a list of wrong answers that receive partial credit. Learners who submit answers that are on the list receive 50% of the problem’s points.
10.28.6.2.1. Configure a List for a Numerical Input Problem¶
To configure a numerical input problem to award partial credit for answers in a list, you add the following attributes to the problem XML.
Add the
partial_credit="list"attribute to the<numericalresponse>element.You can use a list in combination with close answers. Set the attribute to
partial_credit="close,list".Add the
partial_answersattribute to the<responseparam>element. Set its value to one or more answers that should earn 50% of the problem’s points. Separate multiple values by a comma (,).
For example, the following XML shows the numerical problem template updated to provide partial credit for a different answer.
<problem>
<numericalresponse answer="9.3*10^7" partial_credit="close">
<label>How many miles away from Earth is the sun?</label>
<description>Use scientific notation to answer.</description>
<formulaequationinput />
<responseparam partial_answers="150*10^6"/>
</numericalresponse>
</problem>
10.28.7. Add Text after the Numeric Response Field¶
You might want to include a word, phrase, or sentence after the response field in a numerical input problem to help guide your students or resolve ambiguity.
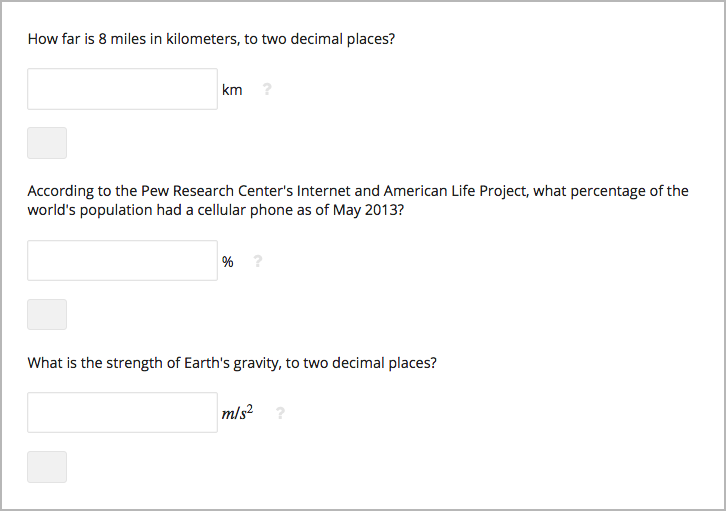
To do this, you use the advanced editor.
In the problem, locate the formulaequationinput element. This element
creates the response field for the problem and is a child of the
numericalresponse element.
To add text after the response field, add the trailing_text attribute
together with the symbol or text that you want to use inside the
formulaequationinput element. An example problem follows with three
questions that use this attribute.
Note
You can use MathJax inside the trailing_text attribute, as the
third question in this example shows. You cannot use HTML inside this
attribute.
<problem>
<numericalresponse answer="12.87">
<label>How far is 8 miles in kilometers?</label>
<formulaequationinput trailing_text="km" />
</numericalresponse>
<numericalresponse answer="91">
<label>According to the Pew Research Center's Internet and American Life
Project, what percentage of the world's population had a cellular phone
as of May 2013?</label>
<formulaequationinput trailing_text="%" />
</numericalresponse>
<numericalresponse answer="9.81">
<label>What is the strength of Earth's gravity, to two decimal places?</label>
<formulaequationinput trailing_text="\(m/s^{2}\)" />
</numericalresponse>
</problem>
10.28.8. Numerical Input Problem OLX Reference¶
10.28.8.1. Templates¶
The following templates represent problems without, and with, a Python script.
10.28.8.1.1. Problem with No Tolerance¶
<problem>
<numericalresponse answer="ANSWER (NUMBER)">
<label>Question text</label>
<description>Optional tip</description>
<formulaequationinput />
<correcthint>Feedback for the correct answer.</correcthint>
<solution>
<div class="detailed-solution">
<p>Explanation</p>
<p>TEXT OF SOLUTION</p>
</div>
</solution>
</numericalresponse>
</problem>
10.28.8.1.2. Answer Created Using a Script¶
Note
The following example includes a Python script. When you add a script to a problem component, make sure that it is not indented. A “jailed code” error message appears when you save the problem in Studio if the script element is indented.
<problem>
<numericalresponse answer="$computed_response">
<label>Question text</label>
<description>Optional tip</description>
<responseparam type="tolerance" default="0.0001" />
<script type="loncapa/python">
computed_response = math.sqrt(math.fsum([math.pow(math.pi,2), math.pow(math.e,2)]))
</script>
<formulaequationinput />
<correcthint>Feedback for the correct answer.</correcthint>
<solution>
<div class="detailed-solution">
<p>Explanation</p>
<p>TEXT OF SOLUTION</p>
</div>
</solution>
</numericalresponse>
</problem>
10.28.8.2. Elements¶
For numerical input problems, the <problem> element can include this
hierarchy of child elements.
<numericalresponse>
<label>
<description>
<formulaequationinput>
<additional_answer>
<correcthint>
<responseparam>
<script>
<solution>
<demandhint>
<hint>
In addition, standard HTML tags can be used to format text.
10.28.8.2.1. <numericalresponse>¶
Required. Indicates that the problem is a numerical input problem.
The <numericalresponse> element is similar to the <formularesponse>
element used by the math expression input problem
type, but the <numericalresponse> element does not allow unspecified
variables.
10.28.8.2.1.1. Attributes¶
| Attribute | Description |
|---|---|
answer |
Required. The correct answer to the problem, given as a mathematical expression. |
partial_credit |
Optional. Specifies the type of partial credit given. close,
list, or a combination of both in any order separated by a comma (,). |
Note
If you include a variable name preceded with a dollar sign
($) in the problem answer, you can include a script in the problem that
computes the expression in terms of that variable.
The grader evaluates the answer that you provide and the learner’s response in the same way. The grader also automatically simplifies any numeric expressions that you or a learner provides. Answers can include simple expressions such as “0.3” and “42”, or more complex expressions such as “1/3” and “sin(pi/5)”.
10.28.8.2.1.2. Children¶
<label><description><formulaequationinput><additional_answer><responseparam><correcthint><script><solution>
10.28.8.2.2. <label>¶
Required. Identifies the question or prompt. You can include HTML tags within this element.
10.28.8.2.2.1. Attributes¶
None.
10.28.8.2.2.2. Children¶
None.
10.28.8.2.3. <description>¶
Optional. Provides clarifying information about how to answer the question. You can include HTML tags within this element.
10.28.8.2.3.1. Attributes¶
None.
10.28.8.2.3.2. Children¶
None.
10.28.8.2.4. <formulaequationinput>¶
Required. Creates a response field in the LMS where learners enter a response.
Note
Some older problems use a <textline math="1" /> element instead of
<formulaequationinput>. However, the <textline math="1" />
element has been deprecated. All new problems should use the
<formulaequationinput> element.
10.28.8.2.4.1. Attributes¶
| Attribute | Description |
|---|---|
size |
Optional. Defines the width, in characters, of the response field in the LMS. |
trailing_text |
Optional. Specified text to appear immediately after the response field. |
10.28.8.2.4.2. Children¶
None.
10.28.8.2.5. <additional_answer>¶
Optional. Specifies an additional correct answer for the problem. A problem can contain an unlimited number of additional answers.
10.28.8.2.5.1. Attributes¶
| Attribute | Description |
|---|---|
answer |
Required. The alternative correct answer. |
10.28.8.2.5.2. Children¶
correcthint
10.28.8.2.6. <responseparam>¶
Specifies a tolerance, or margin of error, for an answer.
10.28.8.2.6.1. Attributes¶
| Attribute | Description |
|---|---|
type |
Optional. "tolerance" defines a tolerance for a number. |
default |
|
partial_range |
Optional. For partial credit problems of type="close", a
multiplier for the tolerance. Default is 2. |
partial_answers |
|
10.28.8.2.6.2. Children¶
None.
10.28.8.2.7. <correcthint>¶
Optional. Specifies feedback to appear after the learner submits the correct answer.
10.28.8.2.7.1. Attributes¶
| Attribute | Description |
label |
Optional. The text of the custom feedback label. |
10.28.8.2.7.2. Children¶
None.
10.28.8.2.8. <script>¶
Optional. Specifies a script that the grader uses to evaluate a learner’s
response. A problem behaves as if all of the code in all of the <script>
elements were in a single <script> element. Specifically, any variables
that are used in multiple <script> elements share a namespace and can be
overridden.
As with all Python, indentation matters, even though the code is embedded in XML.
10.28.8.2.8.1. Attributes¶
| Attribute | Description |
|---|---|
type |
Required. Must be set to loncapa/python. |
10.28.8.2.8.2. Children¶
None.
10.28.8.2.9. <solution>¶
Optional. Identifies the explanation or solution for the problem, or for one of the questions in a problem that contains more than one question.
This element contains an HTML division <div>. The division contains one or
more paragraphs <p> of explanatory text.