8.24. Numerical Input¶
Numerical input problems are the simpler of the two mathematics tools that Studio offers. In these problems, students enter numbers or specific and relatively simple mathematical expressions to answer a question. The text that the students enter is converted to a symbolic expression that appears below the response field.
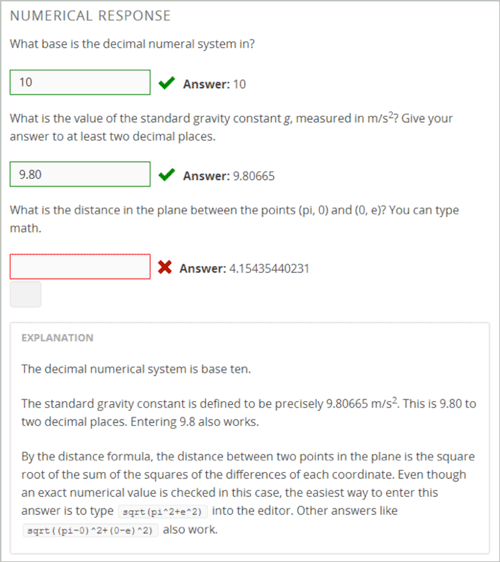
Note that students’ responses don’t have to be exact for these problems. You can specify a margin of error, or tolerance. You can also specify a correct answer explicitly, or use a Python script. For more information, see the instructions below.
Responses for numerical input problems can include integers, fractions, and constants such as pi and g. Responses can also include text representing common functions, such as square root (sqrt) and log base 2 (log2), as well as trigonometric functions and their inverses, such as sine (sin) and arcsine (arcsin). For these functions, the text that the student enters is converted into mathematical symbols. The following example shows the way the system renders students’ text responses in numerical input problems.
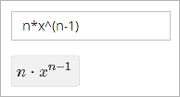
For more information about characters that students can enter, see Math Response Formatting for Students.
8.24.1. Create a Numerical Input Problem¶
You can create numerical problems in the Simple Editor or in the Advanced Editor regardless of the answer to the problem. If the text of your problem doesn’t include any italics, bold formatting, or special characters, you can create the problem in the Simple Editor. If the text of your problem contains special formatting or characters, or if your problem contains a Python script, you’ll use the Advanced Editor.
For example, the following example problems require the Advanced Editor.
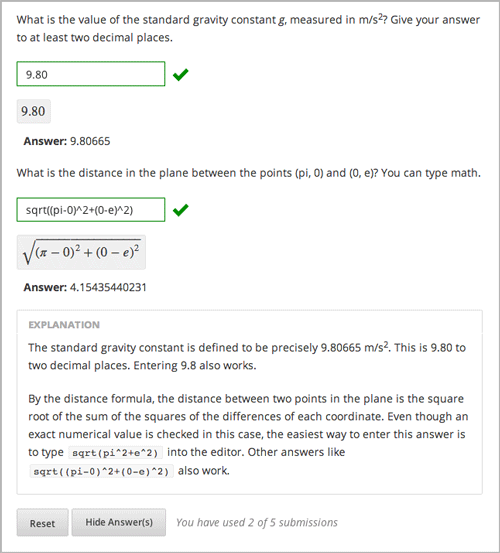
For more information about including a Python script in your problem, see Write-Your-Own-Grader Problem.
8.24.1.1. Simple Editor¶
- Under Add New Component, click Problem.
- In the Select Problem Component Type screen, click Numerical Input on the Common Problem Types tab.
- When the new Problem component appears, click Edit.
- In the component editor, replace the sample problem text with your own text.
- Determine the text of the problem to use as a label, and then surround that text with two sets of angle brackets (>><<).
- Select the text of the answer, and then click the numerical input button.

When you do this, an equal sign appears next to the answer.
(Optional) Specify a margin of error, or tolerance. You can specify a percentage, number, or range.
- To specify a percentage on either side of the correct answer, add +-NUMBER% after the answer. For example, if you want to include a 2% tolerance, add +-2%.
- To specify a number on either side of the correct answer, add +-NUMBER after the answer. For example, if you want to include a tolerance of 5, add +-5.
- To specify a range, use brackets [] or parentheses (). A bracket indicates that range includes the number next to it. A parenthesis indicates that the range does not include the number next to it. For example, if you specify [5, 8), correct answers can be 5, 6, and 7, but not 8. Likewise, if you specify (5, 8], correct answers can be 6, 7, and 8, but not 5.
In the component editor, select the text of the explanation, and then click the explanation button to add explanation tags around the text.

On the Settings tab, specify the settings that you want.
Click Save.
For the first example problem above, the text in the Problem component is the following.
>>What base is the decimal numeral system in?<<
= 10
[explanation]
The decimal numerial system is base ten.
[explanation]
8.24.1.2. Advanced Editor¶
To create this problem in the Advanced Editor, click the Advanced tab in the Problem component editor, and then replace the existing code with the following code.
Problem Code:
<problem>
<p><b>Example Problem</b></p>
<p>What base is the decimal numeral system in?
<numericalresponse answer="10">
<formulaequationinput label="What base is the decimal numeral system in?"/>
</numericalresponse>
</p>
<p>What is the value of the standard gravity constant <i>g</i>, measured in m/s<sup>2</sup>? Give your answer to at least two decimal places.
<numericalresponse answer="9.80665">
<responseparam type="tolerance" default="0.01" />
<formulaequationinput label="Give your answer to at least two decimal places"/>
</numericalresponse>
</p>
<!-- The following uses Python script spacing. Make sure it isn't indented when you add it to the Problem component. -->
<script type="loncapa/python">
computed_response = math.sqrt(math.fsum([math.pow(math.pi,2), math.pow(math.e,2)]))
</script>
<p>What is the distance in the plane between the points (pi, 0) and (0, e)? You can type math.
<numericalresponse answer="$computed_response">
<responseparam type="tolerance" default="0.0001" />
<formulaequationinput label="What is the distance in the plane between the points (pi, 0) and (0, e)?"/>
</numericalresponse>
</p>
<solution>
<div class="detailed-solution">
<p>Explanation</p>
<p>The decimal numerical system is base ten.</p>
<p>The standard gravity constant is defined to be precisely 9.80665 m/s<sup>2</sup>.
This is 9.80 to two decimal places. Entering 9.8 also works.</p>
<p>By the distance formula, the distance between two points in the plane is
the square root of the sum of the squares of the differences of each coordinate.
Even though an exact numerical value is checked in this case, the
easiest way to enter this answer is to type
<code>sqrt(pi^2+e^2)</code> into the editor.
Other answers like <code>sqrt((pi-0)^2+(0-e)^2)</code> also work.
</p>
</div>
</solution>
</problem>
8.24.2. Numerical Input Problem XML¶
8.24.2.1. Templates¶
The following templates represent problems with and without a decimal or percentage tolerance.
8.24.2.1.1. Problem with no tolerance¶
<p>TEXT OF PROBLEM
<numericalresponse answer="ANSWER (NUMBER)">
<formulaequationinput label="TEXT OF PROBLEM"/>
</numericalresponse>
</p>
<solution>
<div class="detailed-solution">
<p>TEXT OF SOLUTION</p>
</div>
</solution>
</problem>
8.24.2.1.2. Problem with a decimal tolerance¶
<problem>
<p>TEXT OF PROBLEM
<numericalresponse answer="ANSWER (NUMBER)">
<responseparam type="tolerance" default="NUMBER (DECIMAL, e.g., .02)" />
<formulaequationinput label="TEXT OF PROBLEM"/>
</numericalresponse>
</p>
<solution>
<div class="detailed-solution">
<p>TEXT OF SOLUTION</p>
</div>
</solution>
</problem>
8.24.2.1.3. Problem with a percentage tolerance¶
<problem>
<p>TEXT OF PROBLEM
<numericalresponse answer="ANSWER (NUMBER)">
<responseparam type="tolerance" default="NUMBER (PERCENTAGE, e.g., 3%)" />
<formulaequationinput label="TEXT OF PROBLEM"/>
</numericalresponse>
</p>
<solution>
<div class="detailed-solution">
<p>TEXT OF SOLUTION</p>
</div>
</solution>
</problem>
8.24.2.1.4. Answer created with a script¶
<problem>
<!-- The following uses Python script spacing. Make sure it isn't indented when you add it to the Problem component. -->
<script type="loncapa/python">
computed_response = math.sqrt(math.fsum([math.pow(math.pi,2), math.pow(math.e,2)]))
</script>
<p>TEXT OF PROBLEM
<numericalresponse answer="$computed_response">
<responseparam type="tolerance" default="0.0001" />
<formulaequationinput label="TEXT OF PROBLEM"/>
</numericalresponse>
</p>
<solution>
<div class="detailed-solution">
<p>TEXT OF SOLUTION</p>
</div>
</solution>
</problem>
8.24.2.2. Tags¶
<numericalresponse>(required): Specifies that the problem is a numerical input problem.<formulaequationinput />(required): Provides a response field where the student enters a response.<responseparam>(optional): Specifies a tolerance, or margin of error, for an answer.<script>(optional):
Note
Some older problems use the <textline math="1" /> tag instead of the <formulaequationinput /> tag. However, the <textline math="1" /> tag has been deprecated. All new problems should use the <formulaequationinput /> tag.
Tag: <numericalresponse>
Specifies that the problem is a numerical input problem. The <numericalresponse> tag is similar to the <formularesponse> tag, but the <numericalresponse> tag does not allow unspecified variables.
Attributes
Attribute Description answer (required) The correct answer to the problem, given as a mathematical expression. Note
If you include a variable name preceded with a dollar sign ($) in the problem, you can include a script in the problem that computes the expression in terms of that variable.
The grader evaluates the answer that you provide and the student’s response in the same way. The grader also automatically simplifies any numeric expressions that you or a student provides. Answers can include simple expressions such as “0.3” and “42”, or more complex expressions such as “1/3” and “sin(pi/5)”.
Children
<responseparam><formulaequationinput>
Tag: * <formulaequationinput>
Creates a response field in the LMS where students enter a response.
Attributes
Attribute Description label (required) Specifies the name of the response field. size (optional) Defines the width, in characters, of the response field in the LMS. Children
(none)
Tag: <responseparam>
Specifies a tolerance, or margin of error, for an answer.
Attributes
Attribute Description type (optional) “tolerance”: Defines a tolerance for a number default (optional) A number or a percentage specifying a numerical or percent tolerance. Children
(none)
Tag: <script>
Specifies a script that the grader uses to evaluate a student’s response. A problem behaves as if all of the code in all of the script tags were in a single script tag. Specifically, any variables that are used in multiple <script> tags share a namespace and can be overriden.
As with all Python, indentation matters, even though the code is embedded in XML.
Attributes
Attribute Description type (required) Must be set to “loncapa/python”. Children
(none)